k-dtree

A K-D Tree(also called as K-Dimensional Tree) is a binary search tree where data in each node is a K-Dimensional point in space. ... A non-leaf node in K-D tree divides the space into two parts, called as half-spaces.

• Invented in 1970s by Jon Bentley
• Name originally meant “3d-trees, 4d-trees, etc” where k was the # of dimensions
• Now, people say “kd-tree of dimension d”
• Idea: Each level of the tree compares against 1
• dimension.
• Let’s us have only two children at each node (instead of 2d)

How to determine if a point will lie in the left subtree or in right subtree?

If the root node is aligned in planeA, then the left subtree will contain all points whose coordinates in that plane are smaller than that of root node. Similarly, the right subtree will contain all points whose coordinates in that plane are greater-equal to that of root node.

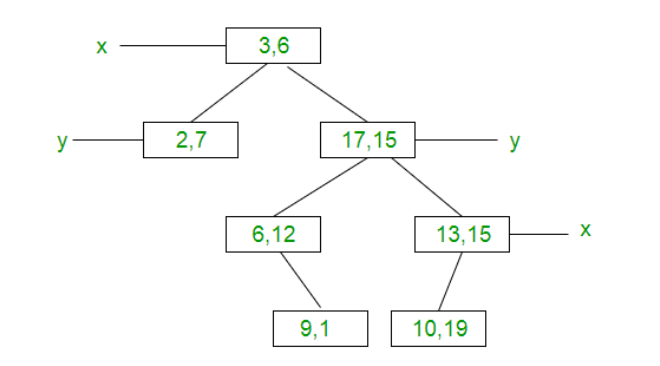
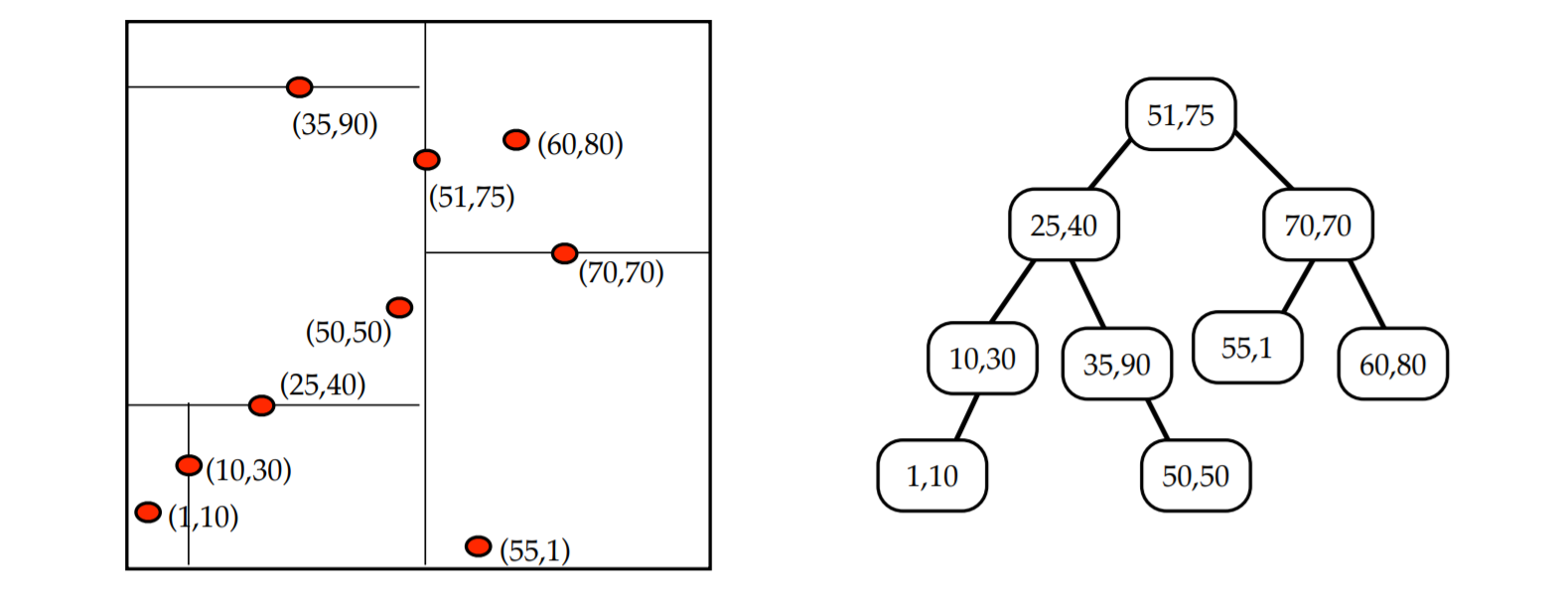
Creation of a 2-D Tree:

Consider following points in a 2-D plane:

(3, 6), (17, 15), (13, 15), (6, 12), (9, 1), (2, 7), (10, 19)

1. Insert (3, 6): Since tree is empty, make it the root node.
2. Insert (17, 15): Compare it with root node point. Since root node is X-aligned, the X-coordinate value will be compared to determine if it lies in the rightsubtree or in the right subtree. This point will be Y-aligned.
3. Insert (13, 15): X-value of this point is greater than X-value of point in root node. So, this will lie in the right subtree of (3, 6). Again Compare Y-value of this point with the Y-value of point (17, 15) (Why?). Since, they are equal, this point will lie in the right subtree of (17, 15). This point will be X-aligned.
4. Insert (6, 12): X-value of this point is greater than X-value of point in root node. So, this will lie in the right subtree of (3, 6). Again Compare Y-value of this point with the Y-value of point (17, 15) (Why?). Since, 12 < 15, this point will lie in the left subtree of (17, 15). This point will be X-aligned.
5. Insert (9, 1):Similarly, this point will lie in the right of (6, 12).
6. Insert (2, 7):Similarly, this point will lie in the left of (3, 6).
7. Insert (10, 19): Similarly, this point will lie in the left of (13, 15).

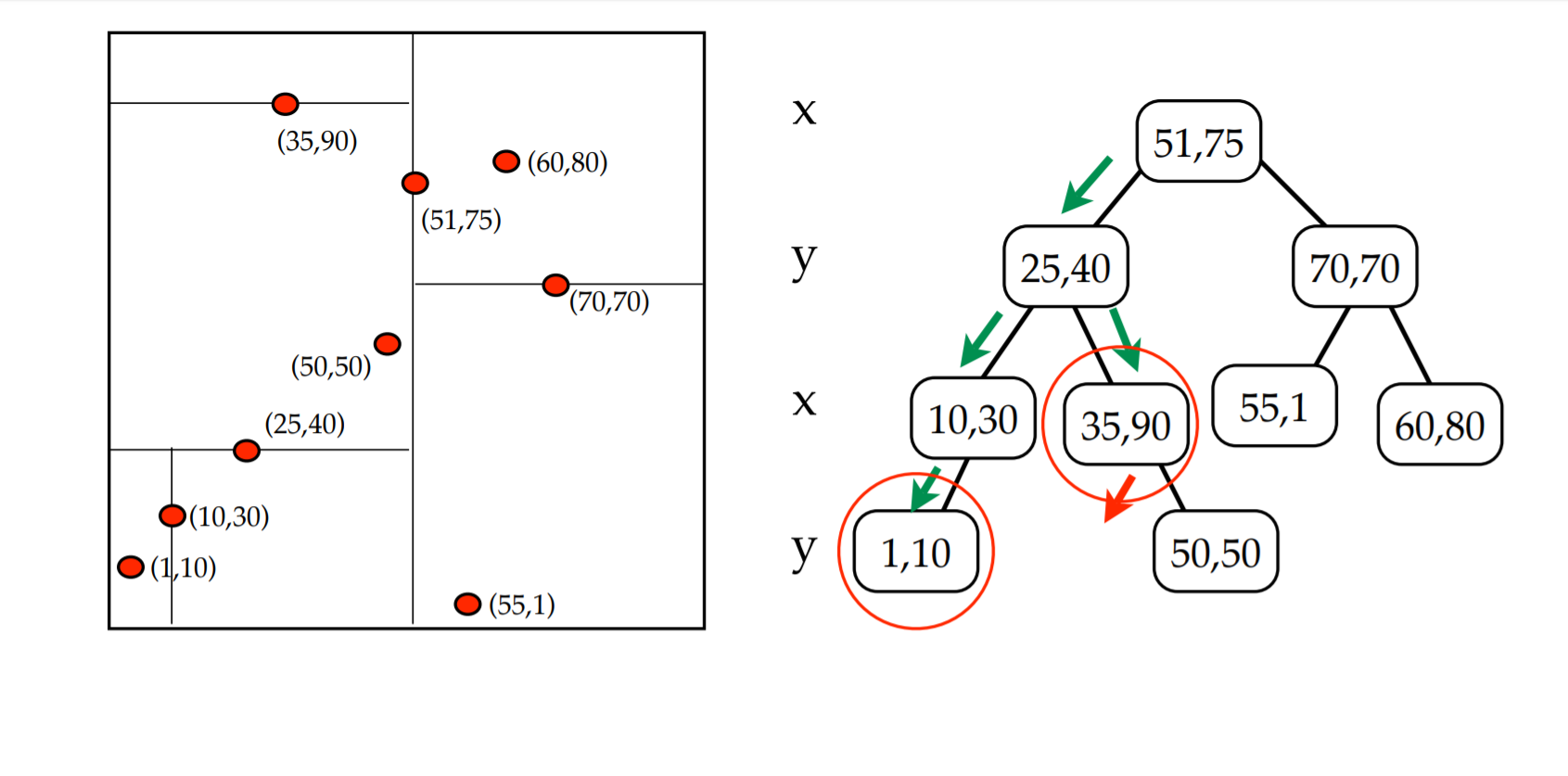
Find Min in kd-trees

FindMin(d): find the point with the smallest value in the dth dimension.

• Recursively traverse the tree
• If cutdim(current_node) = d, then the minimum
• can’t be in the right subtree, so recurse on just the
• left subtree - if no left subtree, then current node is the min for tree
• rooted at this node.
• If cutdim(current_node) ≠ d, then minimum could
• be in either subtree, so recurse on both subtrees. - (unlike in 1-d structures, often have to explore several paths down the tree)

FindMin(x-dimension):

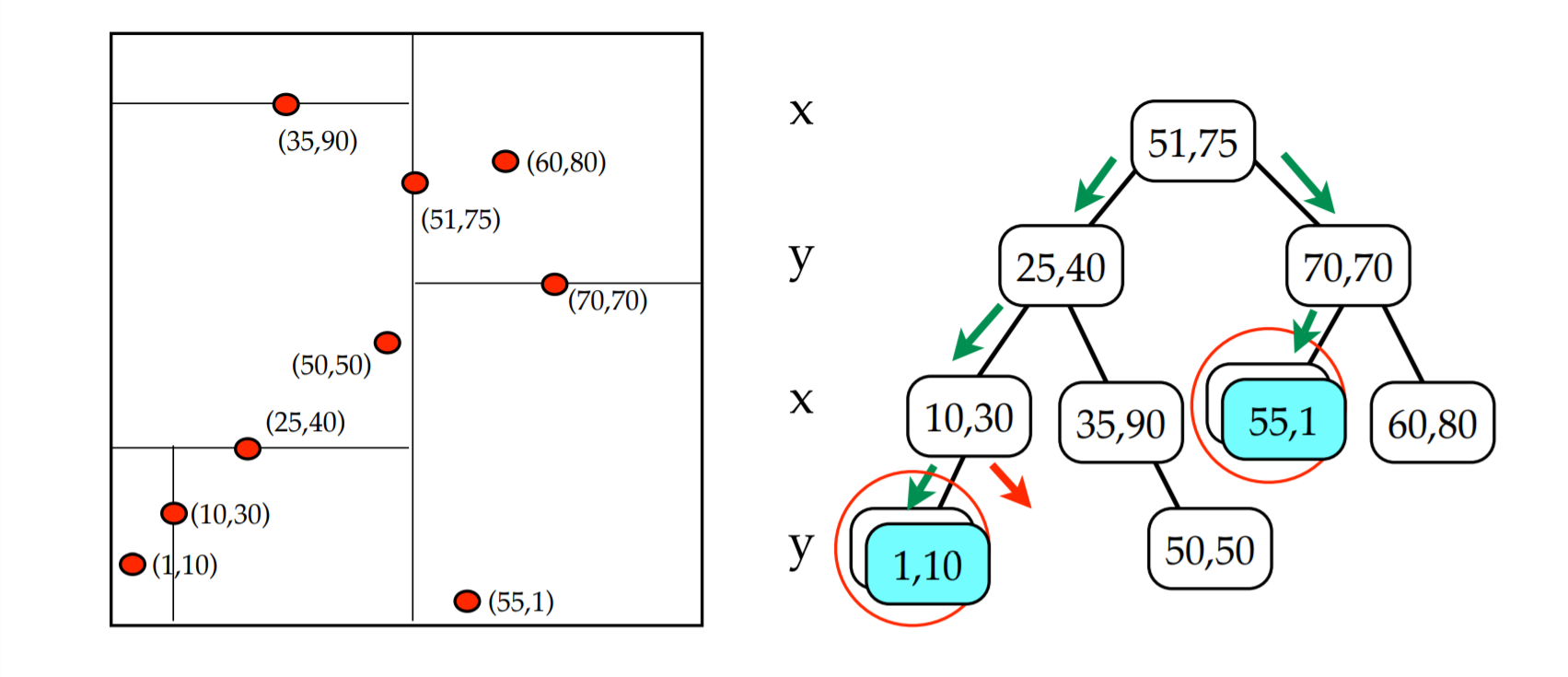
FindMin(Y-dimension):

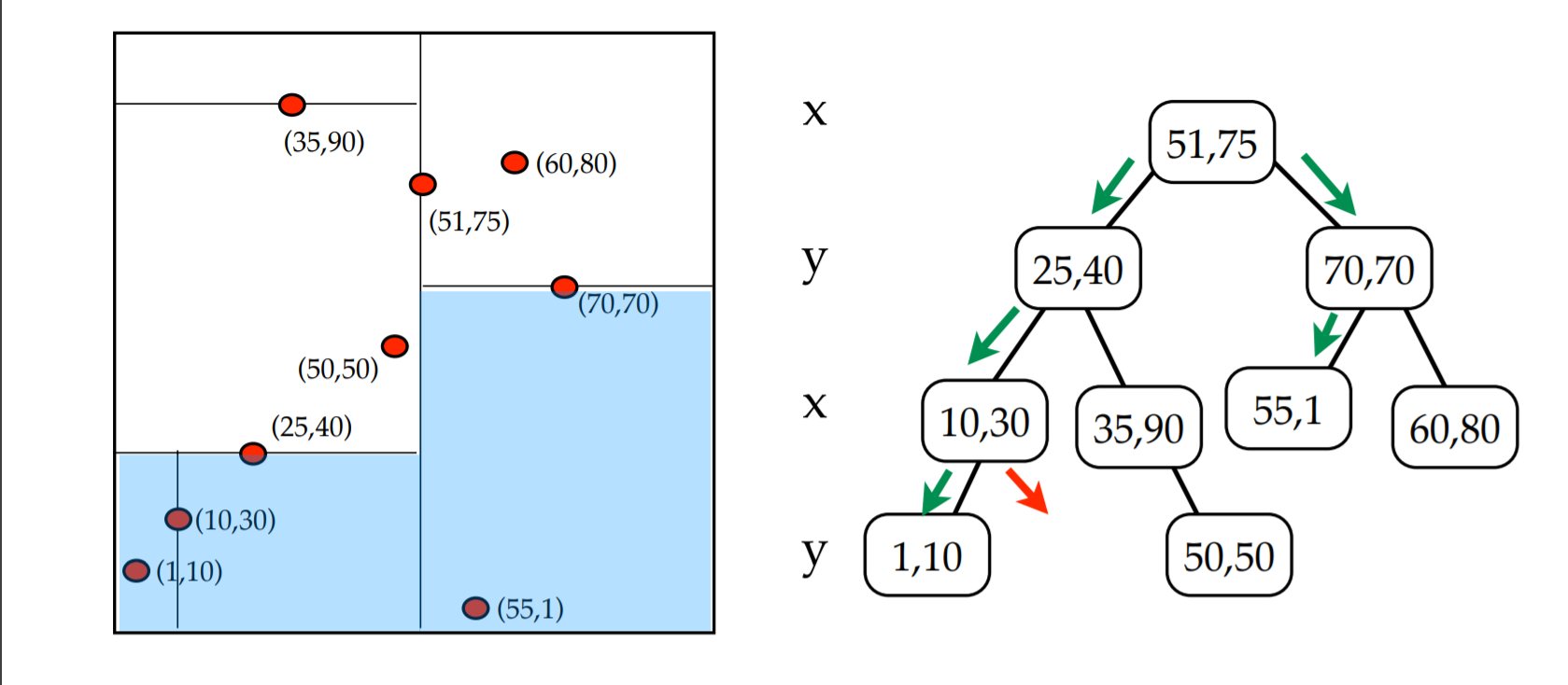
FindMin(y-dimension): space searched

Nearest Neighbor Searching in kd-trees

Nearest Neighbor Queries are very common: given a point Q find the point P in the data set that is closest to Q.

Doesn’t work: find cell that would contain Q and return the point it contains.

• Reason: the nearest point to P in space may be far from P in the tree:
• E.g. NN(52,52):

kd-Trees Nearest Neighbor

Idea: traverse the whole tree, BUT make two modifications to prune to search space

1. Keep variable of closest point C found so far. Prune subtrees once their bounding boxes say that they can’t contain any point closer than C
2. Search the subtrees in order that maximizes the chance for pruning

Nearest Neighbor Facts

Might have to search close to the whole tree in the worst case. [O(n)] • In practice, runtime is closer to:

• O(2d + log n)
• log n to find cells “near” the query point
• 2d to search around cells in that neighborhood

Advantages of k-d tree

k-d trees help in partitioning space just as binary search trees help in partitioning the real line. k-d trees recursively partition a region of space, creating a binary space partition at each level of the tree.

Disadvantages of K-dtree

Well, KD-trees are really cool. They're a very intuitive way to think about storing data, and as we saw, they could lead to help us find relevant information way sooner. But there are few issues. KD-trees are not the simplest things to implement.