t-sne
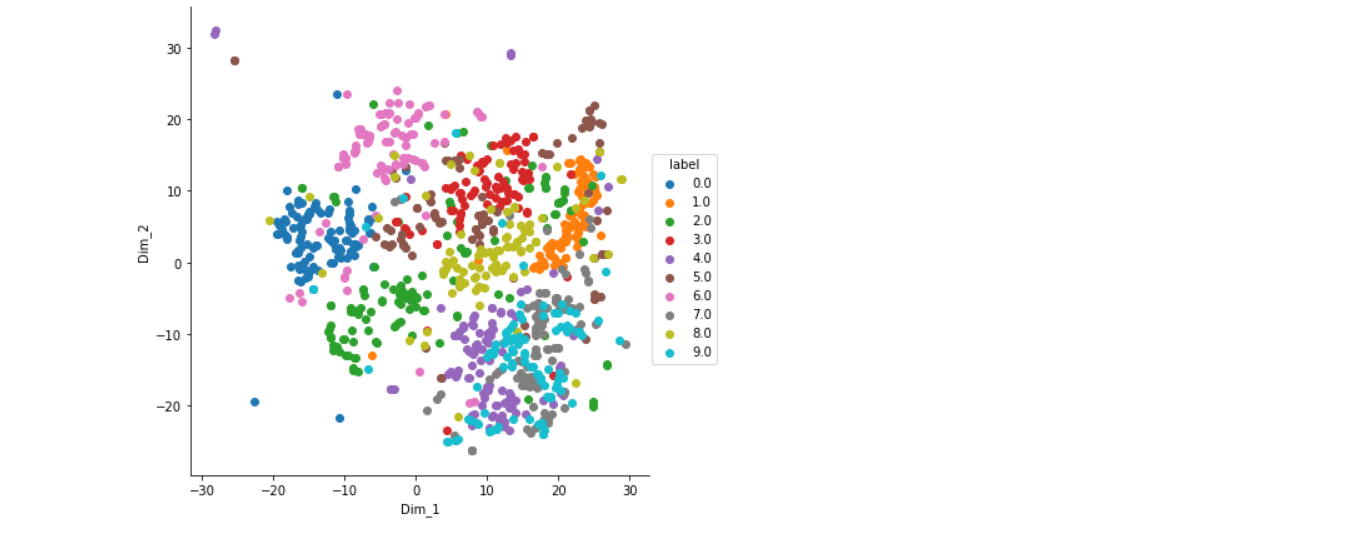
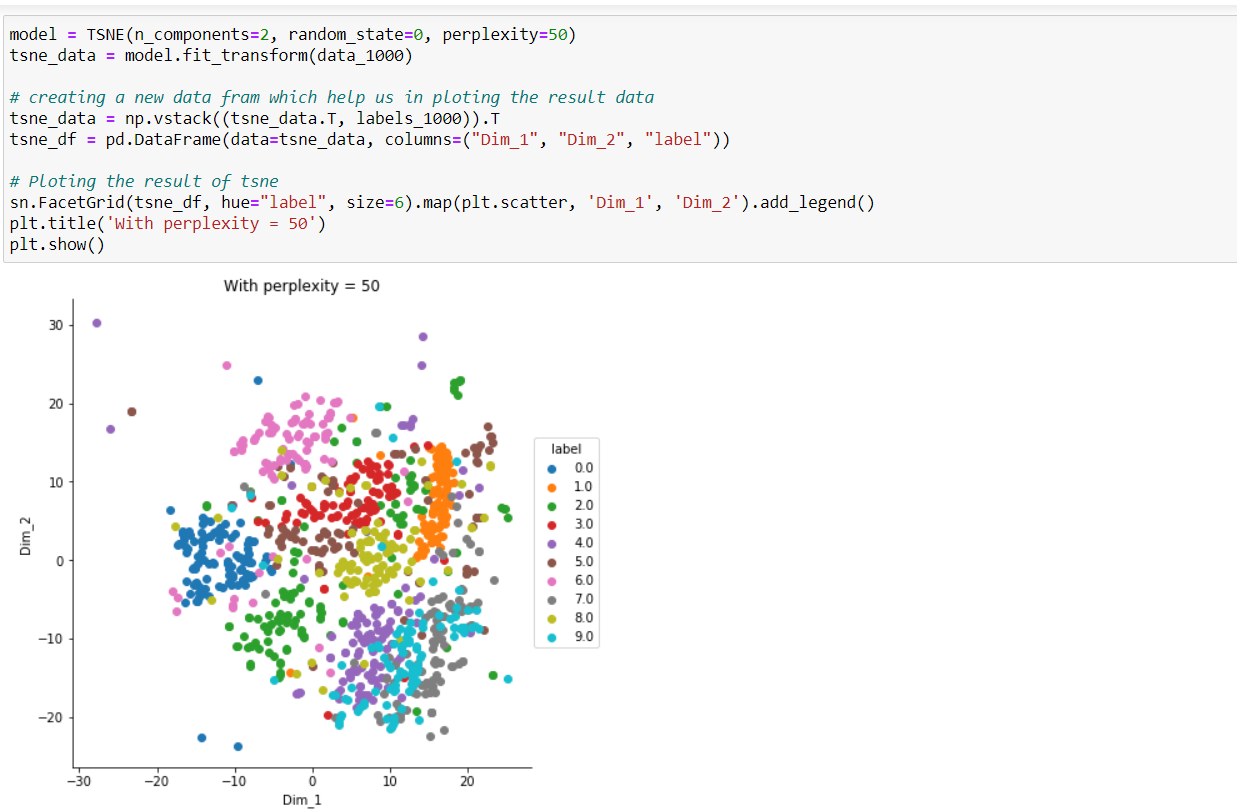
t-Stochastic Neighbor Embedding (t-SNE) used for Visualizing high-dimensional data by projecting it into a low-dimensional space is a classic operation that anyone working with data has probably done at least once in their life. There are a huge variety of methods for reducing dimensionality, but one very popular method is t-SNE, a method proposed by Geoffry Hinton's group back in 2008
- t-SNE creates a probability distribution using the Gaussian distribution that defines the relationships between the points in high-dimensional space.
- t-SNE uses the Student t-distribution to recreate the probability distribution in low-dimensional space. This prevents the crowding problem, where points tend to get crowded in low-dimensional space due to the curse of dimensionality.
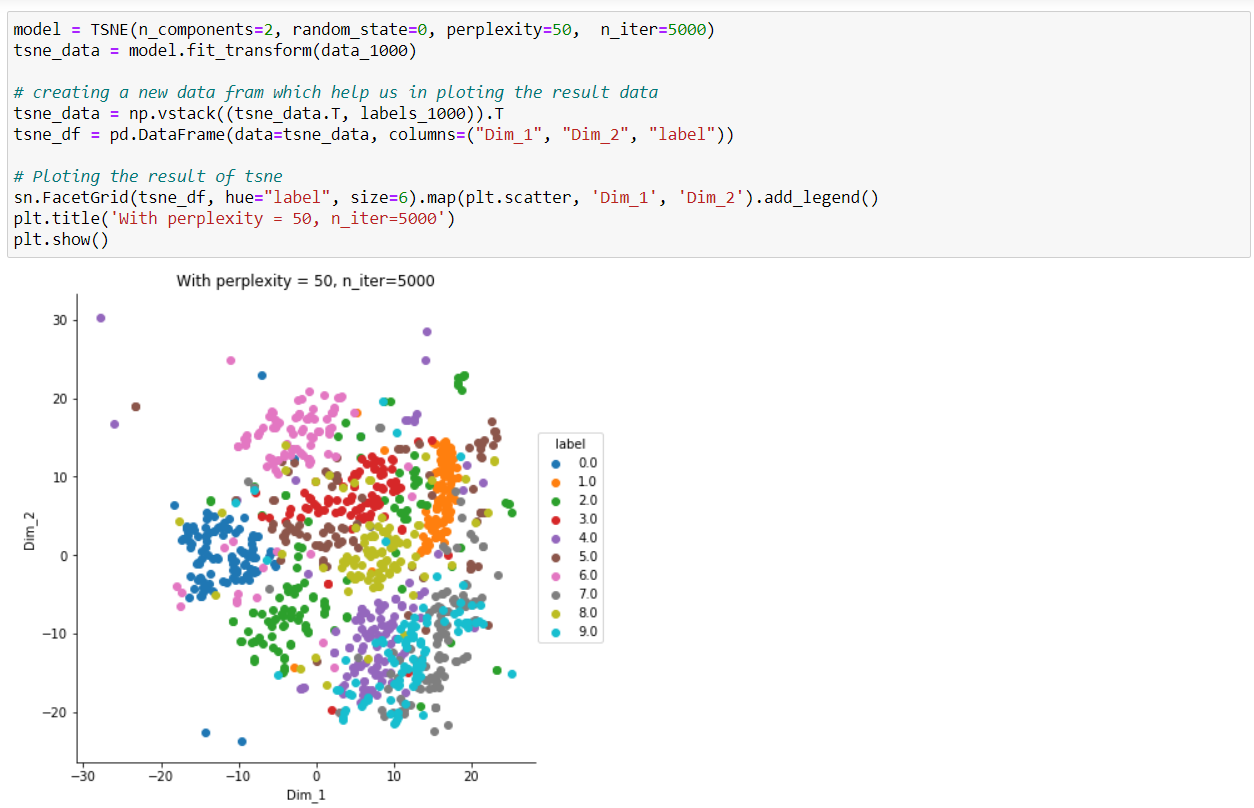
- t-SNE optimizes the embeddings directly using gradient descent. The cost function is non-convex though, meaning there is the risk of getting stuck in local minima. t-SNE uses multiple tricks to try to avoid this problem.
Applications:
- computer security research
- music analysis
- cancer research
- bioinformatics
- biomedical signal processing
Advantages of t-SNE
1.Handles Non Linear Data Efficiently:
t-SNE works well on non-linear data. It is a very effective non-linear dimensionality reduction algorithm.
2.Preserves Local and Global Structure:
t-SNE is capable to preserve local and global structure of the data. This means, roughly, that points which are close to one another in the high-dimensional dataset, will tend to be close to one another in the low dimension. On the other hand, PCA finds new dimensions that explain most of the variance in the data. So, it cares relatively little about local neighbors unlike t-SNE.
Limitations of t-SNE
1.Non-convexity of optimization
t-SNE is non-convex, meaning it has multiple local minima and is therefore much more difficult to optimize.
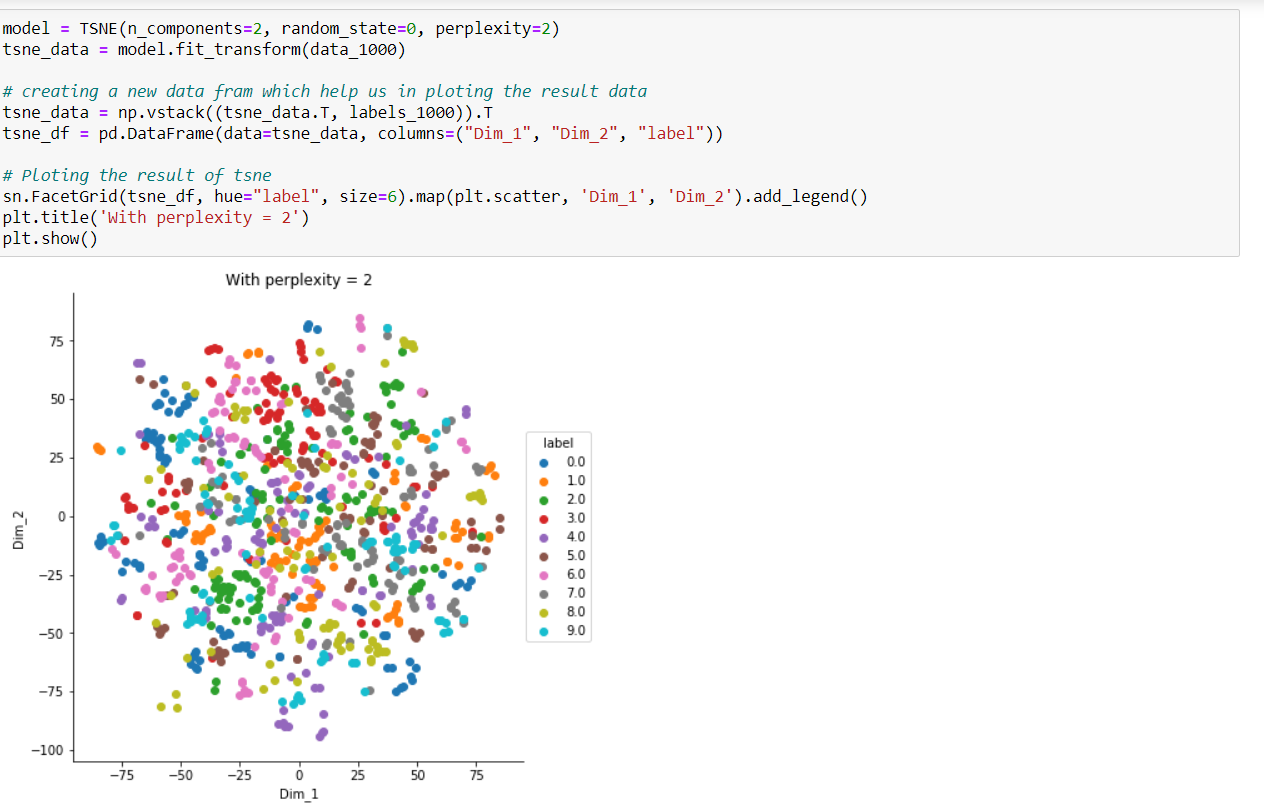
2.Noisy Patterns:
Patterns may be found in random noise as well, so multiple runs of the algorithm with different sets of hyperparameter must be checked before deciding if a pattern exists in the data.
Python Code